JArchive 프로그래밍 일기

펜윅 트리

Fenwick Tree, Binary Indexed Tree(BIT) 라고도 한다.

구간 트리는 구간 합을 빠르게 구하는 데 주로 사용된다. 구간 트리의 진화형태가 펜윅 트리다.

펜윅 트리의 아이디어

"구간 합 대신, 부분 합만을 빠르게 구하는 자료구조를 만들어 두면 구간 합을 계산할 수 있다"

구간 합(range sum) : [3, 6] 과 같은 연속된 구간 합

부분 합(partial sum) : [0, 3] , [0, 8] 과 같이 0번 부터 i까지 합

부분 합 psum의 표현 psum[pos] = A[0] + A[1] + A[2] + ... + A[pos] 로 표현할 수 있다.

구간 [3, 6] 에 대한 합은 psum[6] - psum[2] 로 계산할 수 있다.

구간 [i, j] 에 대한 합은 psum[j] - psum[i-1] 로 계산할 수 있다.

구간 트리와 펜윅 트리의 비교

부분 합(0부터 i까지의 합)만 구한다면, 구간 트리가 미리 계산해 저장하는 상당 수는 필요가 없다.

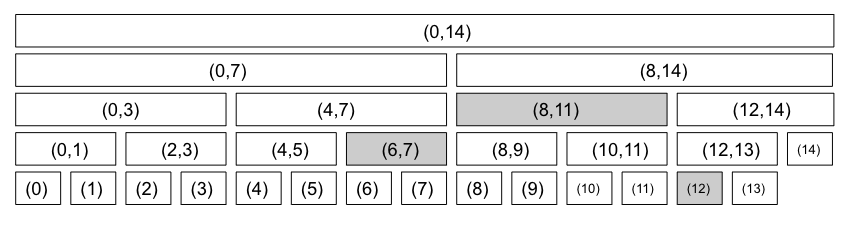
그림 (a) 는 구간트리, (b)는 펜윅 트리이다.

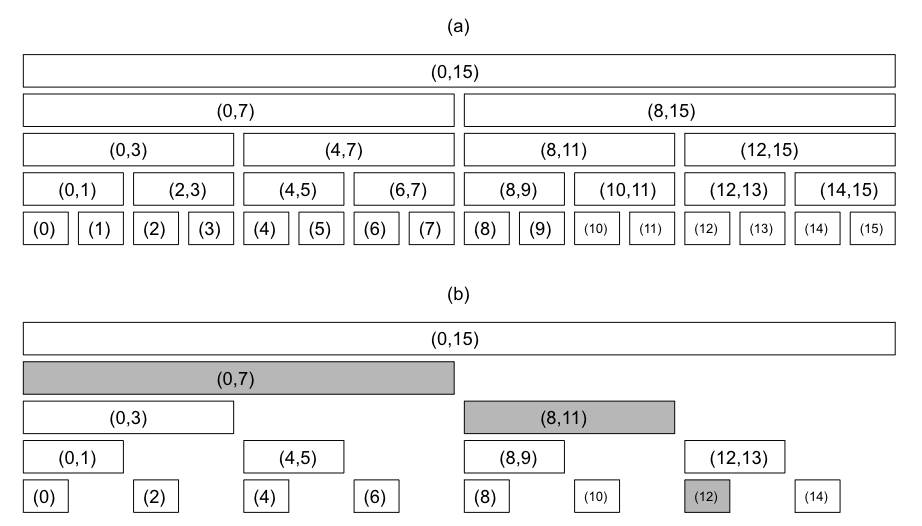
즉, 하나의 긴 구간 밑에 두 개의 작은 구간이 있을 때 두 구간 중 오른쪽 구간은 항상 지워도 된다.

펜윅 트리는 이 대응을 이용해 1차원 배열 하나에 각 구간의 합을 저장한다.

공간복잡도 O(n)

tree[i] = 그림 (b)에서 오른쪽 끝 위치가 A[i]인 구간의 합

구간 합 을 어떻게 계산할까?

A[pos] 까지의 구간합 psum[pos]를 계산하고 싶으면 그림 (b)에서 pos에서 끝나는 구간의 합 tree[pos]를 답에 더한다.

즉, 그림 (b)에서 색칠한 구간 tree[12], tree[11], tree[7]들은 psum[12]를 계산하기 위해 더해야 하는 구간들이다.

• 어떤 부분 합을 구하든 O(logN) 개의 구간 합만 있으면 된다

pos에서 끝나는 구간 다음으로 더해야 할 구간을 어떻게 찾을까?

• 이제 문제는 pos에서 끝나는 구간 다음으로 더해야 할 구간을 어떻게 찾을까 하는 것입니다.
• 펜윅 트리는 각 숫자의 이진수 표현을 이용해 이 문제를 해결합니다.
• 우선 이진수 표현을 위해 배열 A[]와 tree[]의 첫 원소의 인덱스를 1로 바꾼다.
• 모든 원소의 인덱스에 1을 더해 주는 것이다.

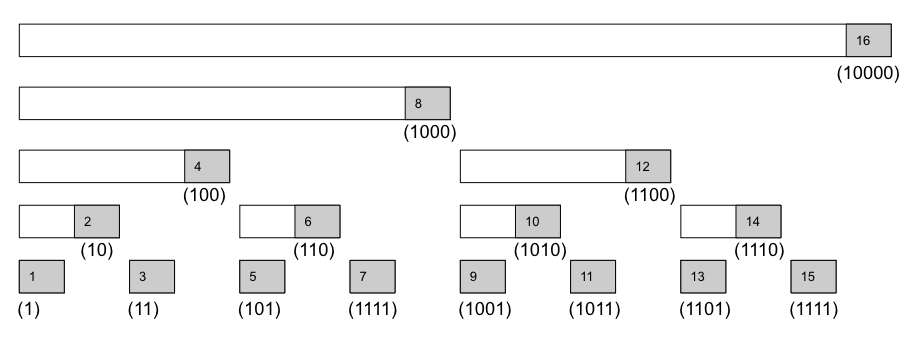
각 구간의 길이는 이진수 표현에서 오른쪽 끝에 있는 0의 개수가 하나 늘 때마다 두 배로 늘어난다.

• psum[7]을 구하기 위해 더해야 하는 숫자는
  • 7에서 끝나는 구간의 합 tree[7] 111
  • 6에서 끝나는 구간의 합 tree[6] 110
  • 4에서 끝나는 구간의 합 tree[4] 100
• 오른쪽 끝 위치의 이진수 표현에서 마지막 비트를 지우면 다음 구간을 쉽게 찾을 수 있음

펜윅 트리 초기화

펜윅 트리를 처음 생성하면 모든 부분 합이 0으로 초기화되므로, 모든 원소가 0인 배열을 표현하게 된다.

• ex) A[5]를 3 늘리고 싶다. 이때 늘려 줘야 할 값들은
  • tree[5] 101
  • tree[6] 110
  • tree[8] 1000
  • tree[16] 10000
• 다른 경우들도 하나하나 시도해 보면 맨 오른쪽에 있는 1인 비트를 스스로에게 더해 주는 연산을 반복하면 해당 위치를 포함하는 구간들을 모두 만날 수 있음
• 예를 들어 110 에서 가장 오른쪽에 있는 비트는 10 이므로, 이를 스스로에게 더하면 1000을 얻을 수 있음

// 펜윅 트리의 구현. 가상의 배열 A[]의 부분 합을 빠르게 구현할 수 있도록 한다. 
// 초기화시에는 A[]의 원소가 전부 0이라고 생각한다.
struct FenwickTree{
    vector<int> tree;
    FenwickTree(int n) : tree(n+1) {}
    // A[0 .. pos]의 부분 합을 구한다.
    int sum(int pos){
        // 인덱스가 1부터 시작한다고 생각 (비트연산 활용을 위해서)
        ++pos;
        int ret = 0;
        while(pos > 0){
            ret += tree[pos];
            // 다음 구간을 찾기 위해 최종 비트를 지운다
            pos &= (pos-1);
        }
        return ret;
    }
    // A[pos]에 val을 더한다
    void add(int pos, int val){
        ++pos;
        while(pos < tree.size()){
            tree[pos] += val;
            pos += (pos & -pos); // -pos : 음수 표현을 위해 비트별 NOT연산을 하고 1을 더한다
        }
    }
};

참고

beakjoon 펜윅트리 포스팅

펜윅트리 vs 구간트리

알고리즘 문제해결전략 (구종만 저)

구간트리

구간트리 (segment tree)

저장된 자료들을 적절히 전처리해 구간에 대한 질문에 빠르게 대답하는 트리

예를 들어, A = {1, 2, 1, 2, 3, 1, 2, 3, 4} 라면,

[2, 4] 구간의 최소치는 1 이다. [6, 8] 구간의 최소치는 2이다.

간단한 알고리즘으로 해당 배열을 순회하여 최소치를 찾아내면 O(n) 의 시간 소요된다.

반면, 해당 배열을 전처리해 구간 트리를 생성하면 같은 연산을 빠르게 구현할 수 있다.

구간트리의 기본 아이디어

구간트리의 기본 아이디어는 주어진 배열의 구간들을 표현하는 이진 트리를 만드는 것이다.

이 때, 루트는 항상 배열의 전체 구간[0, n-1]을 표현한다.

루트의 왼쪽 자식과 오른쪽 자식은 각각 해당 구간의 왼쪽 반과 오른쪽 반을 표현한다.

리프 노드는 길이가 1인 구간을 표현한다.

아래 그림은 배열 길이가 15일 때, 구간 트리의 각 노드가 표현하는 구간들을 보여준다.

각 노드는 해당 구간에 대한 계산 결과를 저장한다.

예를 들어, 구간의 최소치를 구하는 구간트리는 해당 구간의 최소치를 각 노드에 저장한다.

이러한 전처리 과정을 수행해두면 어떤 구간이 주어지더라도 이 구간을 구간들의 합집합으로 표현할 수 있다.

어떤 구간이 주어지건, 답을 찾기 위해 고려해야 하는 구간의 수는 O(logN)

구간트리의 표현

구간 트리를 다뤄보는 일반적인 예제로 '특정 구간의 최소치를 찾는 문제'가 있다.

구간 최소 쿼리(range minimum query, RMQ) 라고 한다.

• 구간 트리는 보통 완전이진트리로 표현한다.

  (그래서 포인터로 연결된 리스트보다는 배열이 메모리 면에서 낫다.)

• 루트 노드를 배열의 1번 원소로 표현한다.

• 노드 i의 왼쪽 자식을 i * 2, 오른쪽 자식을 i * 2 + 1 번째 원소로 표현한다.

• 배열의 길이 정하는 방법

  • 가장 가까운 2의 거듭제곱으로 n을 올림한 뒤, 2를 곱한다.

    (n=6이면, 그 이상의 거듭제곱은 8이다. 따라서 배열의 길이는 16으로 하는 식이다)

    귀찮다면 4n 으로 해도 된다. (4n은 모든 경우에 구간트리가 필요로 하는 배열크기보다 크다)

구간 트리의 초기화(init), 질의(query), 갱신(update) 연산을 알아보자.

1. 구간트리의 초기화 : init()

배열 array[] 가 주어지면, 각 노드마다 해당 구간의 최소치를 계산하는 함수 init()을 구현한다.

현재 구간을 2개로 나눠 재귀호출한 뒤, 두 구간의 최소치 중 더 작은 값을 선택해 해당 구간의 최소치를 계산한다.

// 배열의 구간 최소 쿼리 (RMQ) 문제를 해결하는 구간 트리의 초기화 
struct RMQ{
    // 배열 길이 
    int n;
    // 각 구간의 최소치 
    vector<int> rangeMin;
    RMQ(const vector<int>& array){

    }

    // node를 루트로 하는 서브트리를 초기화 하고, 이 구간의 최소치를 반환.
    int init(const vector<int>& array, int left, int right, int node){
        if(left == right)
            return rangeMin[node] = array[left];
        int mid = (left + right) / 2;
        int leftMin = init(array, left, mid, node * 2);
        int rightMin = init(array, mid +1, right, node * 2 + 1);
        return rangeMin[node] = min(leftMin, rightMin);
    }
};

노드의 수 만큼의 초기화 시간이 소요된다.

배열의 길이 O(n), 노드의 수 O(n), 초기화 시간 복잡도 O(n)

2. 구간트리의 질의 처리 : query()

구간 트리에서의 순회를 이용해 구현한다.

다음과 같이 질의 함수를 정의한다.

int query(left, right, node, nodeLeft, nodeRight) 

/* node가 표현하는 범위 [nodeLeft, nodeRight]와
우리가 최소치를 찾기 원하는 구간 [left, right]의 교집합의 
최소 원소를 반환한다. */

질의 연산은 아래의 3가지 경우를 처리한다.

• 교집합이 공집합인 경우
  • 두 구간은 서로 겹치지 않으니까 반환 값도 없다.
  • 반환 값이 무시되도록 아주 큰 값을 반환하도록 하자.
• 교집합이 [nodeLeft, nodeRight]인 경우
  • [left,right]가 노드가 표현하는 집합을 완전히 포함하는 경우.
  • 이 노드에 미리 계산해 둔 최소치를 곧장 반환하면 된다.
• 이 외의 모든 경우
  • 양쪽 자식 노드에 대해 query()를 재귀 호출한 뒤, 이 두 값 중 더 작은 값을 택해 반환한다.

int query(left, right, node, nodeLeft, nodeRight);

/* node가 표현하는 범위 [nodeLeft, nodeRight]와
우리가 최소치를 찾기 원하는 구간 [left, right]의
교집합의 최소 원소를 반환한다. */

const int _INT_MAX = numeric_limits<int>::max();

// 배열의 구간 최소 쿼리를 해결하기 위한 구간 트리의 구현
struct RMQ{

    int query(int left, int right, int node, int nodeLeft, int nodeRight){
        // 두 구간이 겹치지 않으면 아주 큰 값을 반환한다: 무시됨
        if (right < nodeLeft || nodeRight < left) return _INT_MAX;
        // node가 표현하는 범위가 array[left .. right]에 완전히 포함되는 경우
        if (left <= nodeLeft && nodeRight <= right)
            return rangeMin[node];
        // 양쪽 구간을 나눠서 푼 뒤 결과를 합친다.
        int mid = (nodeLeft + nodeRight) / 2;
        return min(query(left, right, node * 2, nodeLeft, mid),
                   query(left, right, node * 2 +1, mid+1, nodeRight));
    }
    // query()를 외부에서 호출하기 위한 인터페이스
    int query(int left, int right){
        return query(left, right, 1, 0, n-1);
    }
};

아래 그림은 노드가 표현하는 구간과, 최소치를 찾기 원하는 구간이 겹치는 4가지 경우들이다.

노드가 표현하는 구간과 우리가 원하는 구간의 교집합은 짙은 색으로 칠해져 있다.

해당 구간이 노드에 완전히 포함되거나(전부 짙은 색) 아예 포함되지 않는다면(전부 옅은 색) 곧장 종료한다.

그림 (b), (c), (d)에서는 재귀 호출했을 때 양쪽 중 하나는 반드시 곧장 종료한다.

따라서, 그림 (a)처럼 두 구간이 겹쳐야만 양쪽 재귀 호출 둘 중 하나도 곧장 종료하지 않고 탐색을 계속하게 된다.

구간은 절반씩 쪼개지므로 질의 연산의 시간복잡도는 O(logN)이다.

3. 구간트리의 갱신 : update()

원래 배열의 index 위치의 값이 newValue로 바뀌었다고 하자.

이 위치를 포함하는 구간은 트리에 O(logN)개 있을것이다.

따라서 O(logN)개만 다시 계산하면 O(logN)시간에 구간트리를 갱신할 수 있다.

• 갱신 과정은 query()와 init()을 합친 것처럼 구현된다.
• 해당 노드가 표현하는 구간에 index가 포함되지 않는다면 그냥 무시한다.
• 포함된다면 재귀 호출해서 두 자식 구간의 최소치를 계산한 뒤, 그 중에서 최소치를 구한다.

struct RMQ{
    // .. 생략 ..
    // array[index] = newValue로 바뀌었을 때 node를 루트로 하는
    // 구간 트리를 갱신하고 노드가 표현하는 구간의 최소치를 반환한다.
    int update(int index, int newValue, int node, int nodeLeft, int nodeRight){
        // index가 노드가 표현하는 구간과 상관없는 경우엔 무시한다.
        if (index < nodeLeft || nodeRight < index)
            return rangeMin[node];
        // 트리의 리프까지 내려온 경우
        if (nodeLeft == nodeRight) return rangeMin[node] = newValue;
        int mid = (nodeLeft + nodeRight) / 2;
        return rangeMin[node] = min(
                                    update(index, newValue, node*2, nodeLeft, mid),
                                    update(index, newValue, node*2+1,mid+1, nodeRight));
    }
    // update()를 외부에서 호출하기 위한 인터페이스
    int update(int index, int newValue){ 
        return update(index, newValue, 1, 0, n-1);
    }
};

참고

beakjoon 구간 트리

자세한 그림의 구간 트리 설명

간단 정리와 관련예제

구간 트리와 LIS

알고리즘 문제해결전략 (구종만 저)

최소 스패닝 트리 (MST, Minimum cost spanning tree)

스패닝 트리 (spanning tree)

그래프에 있는 모든 정점을 포함하는 부분 그래프

N개의 정점(vertex)와 N-1개의 간선(edge)으로 구성

간선들이 트리 형태이며, 간선들이 모든 정점들을 연결해야 한다.

간선이 트리 형태여야 한다?

선택된 간선들이 사이클(cycle)을 이루지 않는다는 의미

연결 그래프에서 1개 이상의 스패닝 트리를 얻을 수 있다.

DFS, BFS로 얻을 수 있는 스패닝 트리

연결 그래프에서, DFS나 BFS는 암묵적으로 그래프 G의 간선(edge)을 두 개의 집합으로 분리한다.

• T : 스패닝 트리의 edge 집합으로 사용되거나 search 도중에 방문
• N : 남아있는 edge의 집합

아래 그림에서 V(정점)는 8개, E(간선)은 7개이다.

(만약 edge가 vertext의 개수와 같아지면 cycle이 생긴다. )

(a) DFS spanning tree

아직 방문하지 않은 정점으로 향하는 간선이 있으면 그 간선을 무조건 따라간다.

가능한 한 그래프 안으로 '깊이' 간선을 따라가며, 막힌 정점에 도달하면 뒤로 돌아간다.

(b) BFS spanning tree

각 정점을 방문할 때 마다 모든 인접 정점을 검사하므로 V0에서 V1과 V2 쪽으로 순차적으로 두 간선을 방문한다.

최소 스패닝 트리 (minimum cost spanning tree)

가중치 그래프의 스패닝 트리 중, 가중치의 합이 가장 작은 트리

즉, 그래프의 연결성은 유지하되 가장 '저렴한' 그래프

정점이 N개라면, 간선은 N-1개만을 포함한다.

사이클을 만드는 간선은 선택하지 않는다.

최소 스패닝 트리 알고리즘

크루스칼(Kruskal), 프림(Prim), 솔린(Sollin) 알고리즘이 대표적이다. 세 알고리즘 모두 탐욕 알고리즘이다.

탐욕 알고리즘(greedy method)

현재 상황에서 최선의 선택을 한다.

크루스칼과 프림은 상호 배타적 조합(Disjoint Set)을 기본 자료구조로 쓴다.

1. 크루스칼

모든 간선(edge)을 가중치의 오름차순으로 정렬한다.

가중치가 가장 작은 edge를 선택하여 스패닝 트리에 하나씩 추가해 간다.

이 때, 추가하면 사이클이 생기는 간선을 확인하여 제외시킨다.

이렇게 모든 간선을 한 번씩 검사하고 난 뒤 종료한다.

사이클이 발생했는지 판단하는 기준

Union-Find (유니온 파인드) 자료구조를 이용하여 O(1)에 확인 가능

트리에 추가된 정점, 그렇지 않은 정점. 이렇게 두 집합으로 정점들이 나뉜다.

사이클이 생기는 경우, 간선의 양 끝 정점은 같은 컴포넌트(집합)에 속한다.

두 정점이 주어 졌을 때, 이들이 같은 집합에 속하는지 확인(Find)하고,

다른 집합에 속하는 정점이라면 합치는 연산(Union)을 빠르게 지원한다.

크루스칼 알고리즘 탐색 예시

간선 가중치를 정렬한 결과 10, 12, 14, 16, 18, 22, 24, 25, 28

그림 (f) 와 (g) 를 눈여겨보자.

(f) 10, 12, 14, 16을 추가한 트리

(g) 18을 추가하면 사이클이 발생하므로 18을 제외시키고, 22를 추가한다.

2. 프림

하나의 정점으로 구성된 트리에서 시작한다.

여기에 간선을 하나씩 추가하며 스패닝 트리가 될 때까지 키워 간다.

이미 만들어진 트리에 인접한 간선만 고려한다.

(인접한 간선만 고려한다는것 빼고는 크루스칼과 완전히 똑같다. )

시작 정점으로 부터 인접한 정점을 Priority Queue(pq)에 저장하는데, 이때 인접 정점과 간선의 가중치를 함께 저장한다.

프림 알고리즘 탐색 예시

크루스칼 vs 프림

문제 : 최소 스패닝 트리

백준 1197번 최소 스패닝 트리

[참고]

유니온 파인드 개념

[출처]

크루스칼 알고리즘 그림

프림 알고리즘 그림

그래프의 정의와 표현

연결 관계를 표현하기 위한 자료구조

그래프의 정의

그래프 G(V, E)는 어떤 자료나 개념을 표현하는 정점(vertex)의 집합 V와 정점들을 연결하는 간선(edge)들의 집합 E로 구성된 자료구조이다.

그래프는 정점과 간선으로 정의된다. G(V, E)

(cf. 정점의 위치나 간선의 순서 등은 그래프 정의에 포함되지 않는다.)

관련 용어

각 정점에 연결된 간선의 갯수를 차수(degree)라고 한다.

유향 그래프에서는 간선에 방향성이 존재하므로 차수가 두 개로 나뉜다.

정점으로 들어오는 간선의 갯수를 진입차수(in-degree), 정점에서 나가는 간선의 갯수를 진출차수(out-degree) 라고 한다.

그래프의 종류

그래프는 표현하려는 대상에 따라 속성이나 형태의 제약을 추가할 수 있다.

ex) 간선에 방향 속성 추가, 간선에 가중치 속성 추가, 정점을 2개의 그룹으로 나누기 etc.

• 방향 속성
  • 방향그래프(directed graph) 혹은 유향그래프두 정점 v와 u 가 있을 때, v->u 방향의 간선과 u->v 방향의 간선은 서로 다른 간선이다.
  • : 간선에 특정한 방향이 정해진 그래프
  • 무향그래프(undirected graph) : 간선에 방향이 없는 그래프
  • : 간선을 양방향으로 지날 수 있다.
• 가중치 속성
  • 가중치 그래프(weighted graph) : 간선에 가중치(weight) 라는 실수 속성을 부여
• 형태 속성
  • 다중 그래프(multigraph) : 두 정점 사이에 2개 이상의 간선이 존재할 수 있는 그래프
  • 단순 그래프(simple graph) : 두 정점 사이에 간선이 최대 1개만 있는 그래프
• 트리 혹은 루트 없는 트리(unrooted tree)
• : 부모 자식 관계는 없고, 두 정점간의 간선이 1개만 있는 그래프
• 이분 그래프 (bipartite graph)
• : 그래프의 정점들을 겹치지 않는 두 개의 그룹으로 나눈다. 서로 다른 그룹에 속한 정점 간에만 간선이 존재하도록 만든 그래프
• DAG (사이클 없는 방향 그래프, directed acyclic graph): 상호 의존 관계 또는 순서가 정해진 작업들을 표현할 때 활용
• cf) 위상정렬 : 순서가 정해진 작업들에서 순서를 정렬하는 알고리즘 (그래프의 정점을 정렬)
• : 한 점에서 출발해 자기 자신으로 돌아오는 경로(사이클)이 없는 그래프

그래프의 경로

경로(path)란, 끝과 끝이 서로 연결된 간선들을 나열한 것이다.

• 단순 경로(simple path) : 한 정점을 최대 한 번만 지나는 경로 (1-5-4-2)
• 사이클 (cycle 혹은 회로) : 시작한 정점에서 끝나는 경로 (1-5-4-1)

특별한 명시가 없다면 ''경로''는 보통 ''단순 경로''를 의미한다.

• 연결그래프(connected graph) : 모든 정점쌍들에 대해 ''경로''가 존재하는 그래프
• 비연결그래프(disconnected graph) : 특정 정점쌍 사이에 ''경로''가 없는 그래프
• 완전그래프(complete graph) : 모든 정점들이 연결되어 있는 그래프

그래프의 표현 방법

대부분 그래프는 트리에 비해 정적인 용도로 사용된다.

정적이라는 뜻은 새로운 정점이나 간선을 추가/삭제 하는 일이 드물다는 의미다.

따라서 대부분 그래프는 구조의 수정이 어렵더라도 간단하고 메모리를 적게 차지하는 방법으로 구현하는 편이다.

인접 리스트 (adjacency list)

그래프의 각 정점마다 해당 정점에서 나가는 간선의 목록(인접 노드)을 저장해서 그래프를 표현한다.

즉, 각 정점마다 하나의 연결 리스트를 갖는 방식으로 구현한다.

정점 간에 인접한지 list를 모두 확인하는 데에 오래 걸린다.

• 무향 그래프에서 (a, b) 간선은 2 번 저장된다. (a->b) (b->a)는 다르기 때문이다.
• 유향 그래프에서는 (a, b)는 특정 방향이 존재하므로 한 번만 저장된다.

vector<list<int> > adjacent;

간선의 가중치 그래프를 표현하려면?

struct Edge{
    int vertex; // 간선의 반대쪽 끝 정점의 번호 
    int weight; // 간선의 가중치 
}

또는 단순하게 pair STL 이 자주 쓰인다.

pair<int, int>  // 도착 정점, 가중치

가중치 있는 무향 그래프에서 정점, 간선, 가중치 입력받기

(pair 객체 사용)

시작 정점, 도착 정점, 가중치 순으로 입력받는다. 도착정점과 가중치를 pair로 묶는다.

• 그래프 구조 : 정점 개수 5, 간선 개수 6
• 입력 : 시작 정점, 도착 정점, 가중치

- 아래와 같이 입력이 주어진다 -
 5 6 // 정점 개수, 간선 개수
 1 2 1 // 시작 정점, 도착 정점, 가중치 순서
 4 1 5
 2 3 3
 5 2 2
 3 5 4
 4 5 6

• 입력받는 코드

#include <vector>
#include <stdio.h>
using namespace std;

int ver, ed; // 정점, 간선
vector<pair<int,int> > vertex[200];

int main(void){
    scanf("%d %d", &ver, &ed); // 정점 수, 간선 수 입력받기

    for(int i = 0; i < ver; i++){
        int start, end, weight = 0;
        scanf("%d %d %d", &start, &end, &weight);

        vertex[start].push_back(make_pair(end, weight));
        vertex[end].push_back(make_pair(start, weight)); // 무방향 그래프니까 반대 경우도 저장 
    }

}

인접 행렬 (adjacency matrix)

V x V 크기의 2차원 배열로 간선 정보를 저장

• 무향 그래프의 경우: 행렬에 대각선을 그어보면 대칭 모양이 나온다. 대칭 행렬(Symmetric Matrix)
• : 정점 1에서 2, 정점 2에서 1 모두 연결되어 있으므로 1로 표시하고, 연결이 안 된 정점끼리 0으로 표시한다.

• 유향 그래프예를 들어, 정점 6은 가리키고 있는 정점이 5밖에 없다. 정점 6의 인접 정점은 5뿐이다.
• ㅍ
• 
• : 정점 자신이 가리키고 있는 정점에 대해서만 인접해 있다고 표현한다.

vector<vector<bool> > adjacent; // 유향 그래프
vector<vector<int> > adjacent_weight; // 가중치 유향 그래프

• 가중치 가진 유향 그래프
  
• : 간선의 정보를 bool 값 대신 정수나 실수 변수로 쓰면 된다.

인접 리스트와 인접 행렬 표현의 비교

두 방식은 정반대의 특성을 가져서 한 방식의 단점이 다른 방식의 장점이 된다. 구현하려는 알고리즘이나 그래프의 종류에 맞게 사용하자.

• 희소 그래프 : 간선의 수가 V^2 에 비해 적은 그래프
• 밀집 그래프 : 간선의 수가 V^2 에 비례하는 그래프.

그래프와 트리 비교

[참고]

그래프 인접행렬 인접리스트

알고리즘 문제해결전략(도서 종만북 요약)

도움이 되셨다면 '공감'을 눌러주세요 :)

우선순위 큐

보통의 큐 인데 '우선순위'속성을 갖는 자료구조이다.

삽입(Enqueue) 할 때 데이터에 우선순위를 부여한다.

삭제(Dequeue) 할 때 가장 높은 우선순위를 갖는 요소부터 제거한다.

우선순위 큐의 삽입 연산

최소값이나 최대값을 우선순위 기준으로 둔다. 

새 요소가 들어오면 값에 따라 적당한 위치를 탐색해야 한다.

일반적으로 힙 순서 속성을 활용하여 구현한다. 

우선순위 큐의 제거 연산

전단을 제거하면 끝난다.
전단에는 우선순위가 가장 높은 값(여기서는 최소값) 이 있기 때문이다.

다음은 우선순위 큐의 구현에 필요한 '힙'에 관한 내용이다.

힙

힙은 힙 순서 속성을 만족하는 완전이진트리다.

힙은 루트노드를 제거하는 최소값 제거 연산과 새 노드 삽입 연산이 있다.

힙 순서 속성이란?

트리 내의 모든 노드가 부모 노드 보다 큰 값을 가진다는 규칙이다.

완전이진트리란?

최고 깊이를 제외한 모든 깊이의 노드들이 완전히 채워져 있는 이진트리다.

힙에서 가장 작은 데이터를 갖는 노드는 루트 노드이다.

힙에 새 노드 삽입하기

힙 순서 속성을 만족시킬 때 까지 부모와 값을 비교한다.

삽입의 과정은 아래와 같다.

1. 힙의 최고 깊이, 최 우측에 새 노드를 삽입한다.
2. 새 노드의 부모와 새 노드를 비교한다. 부모 노드가 값이 더 크다면 종료한다. 그렇지 않으면 다음을 진행한다.
3. 새 노드가 더 작다면, 부모와 위치를 교환한다. 2번으로 간다.

힙의 최소값 삭제

힙의 최소값은 항상 루트노드다.
루트 노드를 삭제하고 나서, 힙 순서 속성을 유지하는 작업이 주를 이룬다.

최소값 삭제 과정은 아래와 같다.

1. 힙의 루트에 최고 깊이 최 우측 노드를 옮겨온다.
2. 옮겨온 노드의 양쪽 자식을 비교하여, 둘 중에 더 작은 자식과 교환한다.
3. 옮겨온 노드가 양쪽 자식보다 작거나, 잎노드가 되면 연산을 종료한다. 그렇지 않으면 2번, 3번을 반복한다.

힙 예제 구현 해보기

링크드리스트 VS 배열

링크드 리스트로 구현하면, "힙의 가장 마지막 노드"를 찾는데 효율적인 답을 찾기 어렵다.
힙은 완전이진트리 이므로 배열인덱스를 통해 자식과 부모의 위치를 찾아내는 데 좋다.

• k번 인덱스 노드의 양쪽 자식 노드 인덱스 찾기
  • 왼쪽 : 2k + 1
  • 오른쪽 : 2k +2
• k번 노드의 부모 인덱스 찾기
  • (k-1)/2 의 몫

힙의 자료구조

typedef struct Node { // 노드 
    int data;
}HeapNode;

typedef struct Heap { // 힙 
    HeapNode* nodes;
    int capacity; // 힙의 용량
    int usedSize; // 힙에 들어있는 노드 개수  
}Heap;

새 노드 삽입하기

Insert()는 아래 두 함수를 활용한다.

GetParent()는 노드의 인덱스를 입력받아서 부모노드 인덱스를 반환한다.
SwapNodes()는 노드와 부모노드를 교환한다.

void Insert(Heap* H, int newData) { 

    // 1. 최고 깊이 최 우측 노드와 그 것의 부모 노드 인덱스
    int currentPosition = H->usedSize;
    int parentPosition = GetParent(currentPosition);

    // 2. 만약, 힙이 꽉차있다면, 용량 증가 
    if (H->capacity == H->usedSize) {

        H->capacity *= 2;
        H->nodes = (HeapNode*)realloc(H->nodes, sizeof(HeapNode) * H->capacity);
    }

    // 3. 최고 깊이 최 우측 노드에 새 노드 삽입 
    H->nodes[currentPosition].data = newData; 

    // 4. 힙 순서 속성 유지할 때까지 비교 반복
    // 탈출 조건 : 자신이 루트 노드가 된다(인덱스 0). 또는 자신의 값이 부모보다 크거나 같다. 
    while (currentPosition != 0 && H->nodes[currentPosition].data < H->nodes[parentPosition].data) {

        SwapNodes(H, currentPosition, parentPosition); // 자리 교환 

        currentPosition = parentPosition; // 1번 처럼 인덱스 갱신 
        parentPosition = GetParent(currentPosition);
    }

    // 5. 용량 증가
    H->usedSize++; 

    return;
}

힙의 최소값 삭제하기

최소값은 항상 루트노드가 가지고 있다.

1. 함수는 일단 루트노드의 최소값을 기억해 두는 것으로 시작한다.
2. 루트노드 자리에 최고 깊이 최 우측 노드를 복사해서 옮겨둔다.
3. 새로 온 노드는 힙 순서 속성을 만족할 때 까지 자신의 자식 노드와 비교하여 교환을 반복한다.

void DeleteMin(Heap* H, HeapNode* root) { 

    int parentPosition = 0; // 루트노드 자신이 부모로 시작. 루트니까 인덱스 0.
    int leftPosition = 0;
    int rightPosition = 0;

    // root에 최소값을 저장해둔다. 
    memcpy(root, &H->nodes[0], sizeof(HeapNode));
    memset(&H->nodes[0], 0, sizeof(HeapNode));

    H->usedSize--; // 최우측 노드 인덱스 
    SwapNodes(H, 0, H->usedSize); // 루트 자리에 최고 깊이 최우측 노드를 옮겨온다. 

    leftPosition = GetLeftChild(0); // 루트 노드의 왼쪽 자식, 오른쪽 자식 인덱스 
    rightPosition = leftPosition + 1;


    while (1) { // 힙 순서 속성을 만족할 때 까지 루트는 자기 자식과 비교한다.

        int selectedChild = 0; // 1. 부모노드(루트노드)와 교환할 노드의 인덱스를 찾아본다 

        if (leftPosition >= H->usedSize) { 
            // 실제 노드 개수보다 왼쪽자식 인덱스가 같거나 크다 
            // 유의점 : 노드 인덱스는 0부터 시작. 사용량은 1부터 시작
            // 즉, 루트노드는 잎노드가 된 상황. 
            break; 
        }

        if (rightPosition >= H->usedSize) { 
            // 사용 인덱스보다 오른쪽 자식인덱스가 크다
            // 즉, 루트노드에게 오른쪽 자식은 존재하지 않고 왼쪽자식만 있는것임.
            selectedChild = leftPosition; // 타겟은 왼쪽자식 
        }
        else { // 양쪽 자식 존재 

            if (H->nodes[leftPosition].data < H->nodes[rightPosition].data) { 
                // 왼쪽 자식이 작다. 타겟은 왼쪽자식 
                selectedChild = leftPosition; 
            }
            else { // 오른쪽 자식이 작다. 타겟은 오른쪽 자식  
                selectedChild = rightPosition;
            }
        }

        // 2. 값을 보고 교환할 필요가 있는지 확인한다 
        if (H->nodes[selectedChild].data < H->nodes[parentPosition].data) {
            SwapNodes(H, selectedChild, parentPosition);
            parentPosition = selectedChild; // 타겟이 새 부모가 된다. 
        }
        else {
            break;
        }

        // 3. 왼쪽 자식, 오른쪽 자식 인덱스를 갱신한다. 
        leftPosition = GetLeftChild(parentPosition);
        rightPosition = leftPosition + 1;
    }

    // 4. 용량의 반 이하만 쓰고 있다면, 힙 용량을 반으로 줄인다. 
    if (H->usedSize < (H->capacity/2)) {

        H->capacity /= 2; // 줄일 용량 
        H->nodes = (HeapNode*)realloc(H->nodes, sizeof(HeapNode) * H->capacity);

    }

}

힙 예제 전체 코드

헤더파일 heap.h
Insert() 와 Delete()를 포함한 함수가 구현된 heap.cpp
테스트 해보는 heap_test.cpp

heap.h

#ifndef HEAP_H
#define HEAP_H

// 힙 

#include <stdio.h>
#include <memory.h> // memcpy
#include <stdlib.h> // realloc

typedef int ElementType;

typedef struct Node { // 노드 
    ElementType data;
}HeapNode;

typedef struct Heap { // 힙 
    HeapNode* nodes;
    int capacity;
    int usedSize;
}Heap;

Heap* Create(int initialSize);
void Destroy(Heap* H); // 
void Insert(Heap* H, ElementType newData);  // 삽입
void DeleteMin(Heap* H, HeapNode* root); // 최소값 삭제 
int GetParent(int index); // 부모 인덱스 리턴
int GetLeftChild(int index); // 왼쪽 자식 인덱스 리턴
void SwapNodes(Heap* H, int index1, int index2);
void PrintNodes(Heap* H);

#endif

heap.cpp

#include "heap.h"

// 힙 메모리 할당 
Heap* Create(int initialSize) {

    Heap* newHeap = (Heap*)malloc(sizeof(Heap));

    newHeap->nodes = (HeapNode*)malloc(sizeof(HeapNode) * initialSize);
    newHeap->capacity = initialSize;
    newHeap->usedSize = 0;

    printf("size:%d\n", sizeof(HeapNode));

    return newHeap;
}

// 힙 메모리 해제 
void Destroy(Heap* H) {

    free(H->nodes);
    free(H);

    return;
}

// 삽입 
void Insert(Heap* H, int newData) { 

    // 1. 최고 깊이 최 우측 노드와 그 것의 부모 노드 인덱스
    int currentPosition = H->usedSize;
    int parentPosition = GetParent(currentPosition);

    // 2. 만약, 힙이 꽉차있다면, 용량 증가 
    if (H->capacity == H->usedSize) {

        H->capacity *= 2;
        H->nodes = (HeapNode*)realloc(H->nodes, sizeof(HeapNode) * H->capacity);
    }

    // 3. 최고 깊이 최 우측 노드에 새 노드 삽입 
    H->nodes[currentPosition].data = newData; 

    // 4. 힙 순서 속성 유지할 때까지 비교 반복
    // 탈출 조건 : 자신이 루트 노드가 된다(인덱스 0). 또는 자신의 값이 부모보다 크거나 같다. 
    while (currentPosition != 0 && H->nodes[currentPosition].data < H->nodes[parentPosition].data) {

        SwapNodes(H, currentPosition, parentPosition); // 자리 교환 

        currentPosition = parentPosition; // 1번 처럼 인덱스 갱신 
        parentPosition = GetParent(currentPosition);
    }

    // 5. 용량 증가
    H->usedSize++; 

    return;
}


// 최소값 삭제 
void DeleteMin(Heap* H, HeapNode* root) { 

    int parentPosition = 0; // 루트노드 자신이 부모로 시작. 루트니까 인덱스 0.
    int leftPosition = 0;
    int rightPosition = 0;

    // root에 최소값을 저장해둔다. 
    memcpy(root, &H->nodes[0], sizeof(HeapNode));
    memset(&H->nodes[0], 0, sizeof(HeapNode));

    H->usedSize--; // 최우측 노드 인덱스 
    SwapNodes(H, 0, H->usedSize); // 루트 자리에 최고 깊이 최우측 노드를 옮겨온다. 

    leftPosition = GetLeftChild(0); // 루트 노드의 왼쪽 자식, 오른쪽 자식 인덱스 
    rightPosition = leftPosition + 1;


    while (1) { // 힙 순서 속성을 만족할 때 까지 루트는 자기 자식과 비교한다.

        int selectedChild = 0; // 1. 부모노드(루트노드)와 교환할 노드의 인덱스를 찾아본다 

        if (leftPosition >= H->usedSize) { 
            // 실제 노드 개수보다 왼쪽자식 인덱스가 같거나 크다 
            // 유의점 : 노드 인덱스는 0부터 시작. 사용량은 1부터 시작
            // 즉, 루트노드는 잎노드가 된 상황. 
            break; 
        }

        if (rightPosition >= H->usedSize) { 
            // 사용 인덱스보다 오른쪽 자식인덱스가 크다
            // 즉, 루트노드에게 오른쪽 자식은 존재하지 않고 왼쪽자식만 있는것임.
            selectedChild = leftPosition; // 타겟은 왼쪽자식 
        }
        else { // 양쪽 자식 존재 

            if (H->nodes[leftPosition].data < H->nodes[rightPosition].data) { 
                // 왼쪽 자식이 작다. 타겟은 왼쪽자식 
                selectedChild = leftPosition; 
            }
            else { // 오른쪽 자식이 작다. 타겟은 오른쪽 자식  
                selectedChild = rightPosition;
            }
        }

        // 2. 값을 보고 교환할 필요가 있는지 확인한다 
        if (H->nodes[selectedChild].data < H->nodes[parentPosition].data) {
            SwapNodes(H, selectedChild, parentPosition);
            parentPosition = selectedChild; // 타겟이 새 부모가 된다. 
        }
        else {
            break;
        }

        // 3. 왼쪽 자식, 오른쪽 자식 인덱스를 갱신한다. 
        leftPosition = GetLeftChild(parentPosition);
        rightPosition = leftPosition + 1;
    }

    // 4. 용량의 반 이하만 쓰고 있다면, 힙 용량을 반으로 줄인다. 
    if (H->usedSize < (H->capacity/2)) {

        H->capacity /= 2; // 줄일 용량 
        H->nodes = (HeapNode*)realloc(H->nodes, sizeof(HeapNode) * H->capacity);

    }

}

// 현재 노드와 부모 노드 교환 
void SwapNodes(Heap* H, int current, int parent) {

    int copySize = sizeof(HeapNode);
    HeapNode* tempNode = (HeapNode*)malloc(sizeof(HeapNode));

    memcpy(tempNode, &H->nodes[current], copySize);
    memcpy(&H->nodes[current], &H->nodes[parent], copySize);
    memcpy(&H->nodes[parent], tempNode, copySize);

    free(tempNode);

    return;
}

int GetParent(int index) { // 부모의 인덱스를 반환 
    return (int)((index - 1) / 2);
}

int GetLeftChild(int index) { // 왼쪽 자식 인덱스 반환 
    return (index * 2) + 1;
}

void PrintNodes(Heap* H) { // 노드 전체 출력 
    int i = 0;

    for (i = 0; i < H->usedSize; i++) {
        printf("%d ", H->nodes[i].data);
    }
    printf("\n");
}

heap_test.cpp

#include "heap.h"

// 힙 

int main(void) {

	Heap* H = Create(3);
	HeapNode minNode;

	Insert(H, 12); // 6개 삽입 
	Insert(H, 87);
	Insert(H, 111);
	Insert(H, 34);
	Insert(H, 16);
	Insert(H, 75);

	PrintNodes(H);

	DeleteMin(H, &minNode); // 삭제 후 출력 하는 것을 반복 
	PrintNodes(H);

	DeleteMin(H, &minNode);
	PrintNodes(H);

	DeleteMin(H, &minNode);
	PrintNodes(H);

	DeleteMin(H, &minNode);
	PrintNodes(H);

	DeleteMin(H, &minNode);
	PrintNodes(H);

	DeleteMin(H, &minNode);
	PrintNodes(H);

	Destroy(H);

	return 0;
}

실행 화면 

힙을 이용한 우선순위 큐 예제

힙은 최소값이나 최대값을 바로 얻어낼 수 있으므로 우선순위 큐 구현에 적합하다.

힙 예제에 썼던 코드와 우선순위 큐 예제가 다른 점은 아래와 같다.

• HeapNode 구조체에 Priority 필드 추가
• HeapNode의 data 필드 자료형을 void*로 변경

헤더파일 priorityQueue.h

함수들을 구현한 priorityQueue.cpp

테스트하는 main 함수 priorityQueue_test.cpp 3개로 구성됬다. 

실행결과 화면 

priorityQueue.h

#ifndef PRIORITYQUEUE_H
#define PRIORITYQUEUE_H

#include <stdio.h>
#include <memory.h>
#include <stdlib.h>

typedef int PriorityType;

typedef struct PQNode {
	PriorityType priority;
	void* data;
}PQNode;

typedef struct PQ {
	
	PQNode* nodes;
	int capacity;
	int usedSize;

}PriorityQueue;

PriorityQueue* PQ_Create(int initialSize);
void PQ_Destory(PriorityQueue* PQ);
void PQ_Enqueue(PriorityQueue* PQ, PQNode newNode);
void PQ_Dequeue(PriorityQueue* PQ, PQNode* root);
int PQ_GetParent(int index);
int PQ_GetLeftChild(int index);
void PQ_SwapNodes(PriorityQueue* PQ, int index1, int index2);
int PQ_IsEmpty(PriorityQueue* PQ);

#endif

priorityQueue.cpp

#include "priorityQueue.h"

// 우선순위 큐 생성 
PriorityQueue* PQ_Create(int initialSize) {
	
	PriorityQueue* PQ = (PriorityQueue*)malloc(sizeof(PriorityQueue));
	PQ->nodes = (PQNode*)malloc(sizeof(PQNode) * initialSize);
	PQ->capacity = initialSize;
	PQ->usedSize = 0;

	return PQ;
}

void PQ_Destory(PriorityQueue* PQ) {

	free(PQ->nodes);
	free(PQ);

	return;
}

// 삽입 
void PQ_Enqueue(PriorityQueue* PQ, PQNode newNode) {

	int currentPosition = PQ->usedSize;
	int parentPosition = PQ_GetParent(currentPosition);

	// 1. 용량 확인 
	if (PQ->usedSize == PQ->capacity) {

		if (PQ->capacity == 0) {
			PQ->capacity = 1;
		}

		PQ->capacity *= 2; // 용량 2배 증가
		PQ->nodes = (PQNode*)realloc(PQ->nodes, sizeof(PQNode) * PQ->capacity);
	}

	// 2. 삽입
	PQ->nodes[currentPosition] = newNode;

	// 3. '힙 순서 속성' 만족시킬 때 까지 후속처리
	while (currentPosition != 0 &&
		PQ->nodes[currentPosition].priority < PQ->nodes[parentPosition].priority) {

		PQ_SwapNodes(PQ, currentPosition, parentPosition); // 자신과 부모 위치 교환 

		currentPosition = parentPosition; // 인덱스 갱신 
		parentPosition = PQ_GetParent(currentPosition);
	}

	PQ->usedSize++;

	return;
}


// 최소값 삭제 
void PQ_Dequeue(PriorityQueue* PQ, PQNode* root) {

	int parentPosition = 0; // 루트노드 자리에서 시작한다. 
	int leftPosition = 0;
	int rightPosition = 0;

	// 1. 루트노드의 값을 root에 저장해둔다. 
	memcpy(root, &PQ->nodes[0], sizeof(PQNode));
	memset(&PQ->nodes[0], 0, sizeof(PQNode)); // 0으로 초기화 

	// 2. 최고 깊이 최우측 노드를 root 자리에 옮긴다. 
	PQ->usedSize--;
	PQ_SwapNodes(PQ, 0, PQ->usedSize);

	leftPosition = PQ_GetLeftChild(0); // 루트의 왼쪽 자식
	rightPosition = leftPosition + 1;  // 루튼의 오른쪽 자식

	// 3. 자신과 자신의 양쪽 자식을 비교 
	while (1) {
		
		int targetPosition = 0;

		// 비교할 자식을 고름 
		if (leftPosition >= PQ->usedSize) { // 자식 없음
			break;
		}
		else if (rightPosition >= PQ->usedSize) { // 왼쪽 자식만 존재 
			targetPosition = leftPosition;
		}
		else {
			// 양쪽 자식 존재 

			if (PQ->nodes[leftPosition].priority < PQ->nodes[rightPosition].priority) {
				targetPosition = leftPosition;
			}
			else {
				targetPosition = rightPosition;
			}

		}

		// 자신과 자식의 값 비교해서 교환 필요 여부 확인 
		if (PQ->nodes[targetPosition].priority < PQ->nodes[parentPosition].priority) {
			PQ_SwapNodes(PQ, targetPosition, parentPosition);
		}
		else {
			break; // 탈출 
		}

		// 인덱스 갱신 
		leftPosition = PQ_GetLeftChild(parentPosition);
		rightPosition = leftPosition + 1;
	}

	// 4. 힙 용량 관리

	if (PQ->usedSize < PQ->capacity / 2) {
		// 용량 감소 

		PQ->capacity /= 2; 
		PQ->nodes = (PQNode*)realloc(PQ->nodes, sizeof(PQNode) * PQ->capacity);
	}

	return;
}

// 노드 교환 
void PQ_SwapNodes(PriorityQueue* PQ, int index1, int index2) {

	int NodeSize = sizeof(PQNode);
	PQNode* tempNode = (PQNode*)malloc(NodeSize);

	memcpy(tempNode, &PQ->nodes[index1], NodeSize);
	memcpy(&PQ->nodes[index1], &PQ->nodes[index2], NodeSize);
	memcpy(&PQ->nodes[index2], tempNode, NodeSize);

	free(tempNode);
	return;
}

int PQ_GetParent(int index) { // 부모 노드 인덱스 반환 
	return (int)((index - 1) / 2);
}
int PQ_GetLeftChild(int index) { //왼쪽 자식 인덱스 반환 
	return (index * 2) + 1;
}

int PQ_IsEmpty(PriorityQueue* PQ) { // 비어서 사용량이 0인지 반환 
	return (0 == PQ->usedSize);
}

priorityQueue_test.cpp

#include "priorityQueue.h"

void PrintNode(PQNode* node) {
	printf("작업명: %s (우선순위:%d)\n", (char*)node->data, node->priority);
}

int main(void) {

	// PQ를 크기를 입력하여 생성한다. 
	PriorityQueue* PQ = PQ_Create(3);

	PQNode Popped;

	PQNode Nodes[7] = {
		{34, (void*)"코딩"},
		{12, (void*)"고객미팅"},
		{87, (void*)"화분물주기"},
		{45, (void*)"문서작성"},
		{35, (void*)"디버깅"},
		{66, (void*)"이닦기"},
	};
	
	// 큐에 넣는다. 
	PQ_Enqueue(PQ, Nodes[0]);
	PQ_Enqueue(PQ, Nodes[1]);
	PQ_Enqueue(PQ, Nodes[2]);
	PQ_Enqueue(PQ, Nodes[3]);
	PQ_Enqueue(PQ, Nodes[4]);
	PQ_Enqueue(PQ, Nodes[5]);

	printf("큐에 남아있는 작업 수 %d\n", PQ->usedSize);

	while (!PQ_IsEmpty(PQ)) {
		PQ_Dequeue(PQ, &Popped);
		PrintNode(&Popped);
	}

	return 0;
}

삽입정렬

삽입정렬이란?

삽입정렬은 크기가 n인 집합일 때,
2개, 3개, 4개 ... n-1개씩 비교대상이 늘어나는 것이 특징이다.

단, 사이클마다 대상 집합이 이미 정렬되어 있는 경우에는 비교가 일어나지 않는다. 그래서 무조건(정렬이 되어 있든 아니든) 비교하는 버블정렬보다 평균적으로는 성능이 좋다.

아래에서 예시로 정렬할 때 오름차순을 목표로 한다.

특징

1.정렬 대상이 처음에는 2개.
사이클을 반복할 때마다 1개씩 커집니다. 최대 n-1까지 커진다.

2.정렬 대상의 가장 오른쪽 요소가 대상 중에서 가장 큰 값인지 확인한다.
그렇지 않다면 그 것의 적절한 위치를 찾아준다. 자신보다 큰 요소를 만날 때 까지 탐색한다.

3.적절한 곳을 찾았다면, 자신보다 큰 요소들을 모두 한칸씩 앞으로 이동시킨다. 그리고 새로 생긴 곳에 위치시킨다.

예시

5 1 6 4 2 3

데이터 집합 크기는 6이다.

일단 비교 대상은 2개다. 5와 1.

가장 오른쪽 요소인 1이 가장 큰값을 가지는지 확인해본다.

1을 뽑는다. 1보다 큰 수 5 앞에 놓아야 한다.

5를 이동시켜서 오른쪽으로 밀어서 공간을 만든다.

빈 곳에 1을 삽입한다.

결과 : 1 5 6 4 2 3

비교 대상은 3개다. 1, 5, 6

가장 오른쪽 요소 6이 가장 큰 값을 가지는지 확인한다. (6을 그 앞의 숫자 5와 비교한다.)

6이 더 크다.

그 앞의 요소들은 이미 정렬을 거친 숫자들이니까 확인할 필요가 없다. (!!)

다음 단계로 넘어간다.

비교 대상은 4개다. 1, 5, 6, 4

가장 오른쪽 요소 4가 가장 큰 값을 가지는지 확인한다. (4를 그 앞의 수 6과 비교한다.)

4가 작으니까 이동이 필요하다.

4를 뽑는다.

6, 5, 1 순으로 탐색해보니까 1 앞에 오면 된다.

5와 6을 오른쪽으로 민다. 빈 공간에 4를 삽입한다.

결과 : 1 4 5 6 2 3

삽입정렬 코딩해보기 1

#include <stdio.h>
#include <string.h>

void InsertionSort(int dataset[], int length){
    int i=0, j=0, target=0;

    for(i=1; i<length; i++){

        if(dataset[i-1] < dataset[i]){
            continue; // 맨 오른쪽 요소가 가장 크다면 정렬이 필요 없다. 
        }

        target = dataset[i]; // 맨 오른쪽 요소의 적절한 위치 탐색시작

        for(j=0; j<i; j++){

            if(dataset[j] > target){
                // 데이터를 쭈욱 민다. 
                memmove(&dataset[j+1], &dataset[j], sizeof(dataset[0])*(i-j));
                dataset[j] = target;
                break;
            }
        }
    }
}

int main(void){

    int dataset[] = {5, 3, 6, 4, 1, 2};
    int length = sizeof(dataset) / sizeof(int);
    int i = 0;

    InsertionSort(dataset, length);

    for(i=0; i<length; i++){
        printf("%d ", dataset[i]);
    }

    return 0;
}

memmove() 함수

메모리에 내용을 이동시키는 함수이다. C표준함수.

배열처럼 연속된 데이터를 이동시킬 때 유용하다.

반복문으로 이 함수의 기능을 구현할 수 있지만 성능이 떨어진다.

void* memmove(void* dest, const void *src, size_tn)

dest: 복사의 대상이 되는 목적지 주소

src: 복사할 원본이 있는 주소

size_tn : 복사할 메모리 길이 (byte)

memmove() 함수는 데이터를 '이동'시키고 memcpy() 함수는 데이터를 '복사'한다.

삽입정렬 코딩해보기 2

memmove() 메모리 복사 없이, 배열의 데이터 복사하는 방식으로 정렬해본다.

i와 j로 만든 이중 for문인데,

i는 1부터 시작한다. 비교 집합의 맨 오른쪽 수가 i인데 temp 변수에 기억해둔다.

j 반복문 안에서, temp 보다 큰 수가 있다면 하나씩 오른쪽으로 당긴다.

적절한 위치를 발견하는 순간 temp에 저장된 값을 삽입한다.

input.txt 입력 설명
첫 번째 줄에 자연수 N(1<=N<=100)이 주어집니다.
두 번째 줄에 N개의 자연수가 공백을 사이에 두고 입력됩니다.
6
11 7 5 6 10 9

출력 설명
오름차순으로 정렬된 수열을 출력합니다.
5 6 7 9 10 11

#include <stdio.h> 

int main(int argc, char** argv){

    int a[100], num=0, temp=0, i=0, j=0;

    freopen("input.txt", "rt", stdin);

    scanf("%d", &num); // 데이터 개수  

    for(i=0; i<num; i++){ // 데이터 저장  
        scanf("%d", &a[i]);
    }

    for(i=1; i<num; i++){ // 오름차순으로 정렬 

        temp = a[i]; // a[i]의 적당한 위치를 탐색 시작  

        for(j=i-1; j >= 0; j--){ // 오른쪽에서 왼쪽으로 순회  

            if(a[j] > temp){  
                a[j+1] = a[j];
            }else{
                break;
            }
        }

        a[j+1] = temp; // 적당한 위치에 삽입. 
    }

    for(i=0; i<num; i++){ // 정렬 결과  
        printf("%d ", a[i]);
    }

    return 0;
}

• 헷갈렸던 부분 정리!

데이터집합이 3 2 4 5 라고 가정한다.

i는 인덱스 1부터 temp 에는 2 가 들어가 있다.
j는 인덱스 i-1부터 시작하니까 0 이 들어가 있다.

for문의 조건을 확인한다.
j는 0보다 크거나 같으니까, 반복문 안의 코드가 실행된다.
3이 2보다 크니까 if문 조건을 만족한다.
그래서 인덱스 1 자리에 인덱스 0의 값이 복사된다.
그 결과 3 3 4 5 가 된다.
반복문 안의 코드 수행이 끝났으니까, j--가 수행된다.
j는 -1이 된다.
다시 for문의 조건을 확인한다. j>=0 을 만족하지 못하니까 반복문을 종료한다.

j는 -1인 채로 남아 있었으니까, arr[j+1] 은 arr[0]을 의미한다.
그래서 인덱스 0 자리에 temp값 2를 넣는다.
그 결과 2 3 4 5 가 된다.

버블정렬

버블 정렬이란?

거품이 보글보글 올라오는 모양처럼 정렬이 일어난다고 해서 버블 정렬이다.

버블 정렬은 '이웃끼리' 교환을 통해 요소를 정렬한다.

한 사이클을 순회할 때 마다 '가장 큰 수'가 자리를 잡게 된다.

예시

5 1 6 4 2 3

제일 왼쪽에 있는 요소 부터 이웃 데이터끼리 비교하여 오름차순으로 정렬한다.

5와 1을 비교한다.

1 5 6 4 2 3

5와 6을 비교한다. 교환이 필요없으므로 넘어간다.

6과 4를 비교한다.

1 5 4 6 2 3

6과 2를 비교한다.

1 5 4 2 6 3

6과 3을 비교한다.

1 5 4 2 3 6

한 사이클이 끝나면, 가장 큰 수가 가장 마지막에 자리를 잡을 수 있다.

보글보글 하면서 가장 큰 수가(6) 마지막에 가 있고.

그 다음 사이클에는 또 보글보글 하면서 그 다음 큰 수(5)가 마지막에 가 있고.

그 다음 사이클에는 보글보글 하면서 그 다음 큰 수(4)가 마지막에 가 있고. ... 를 반복하게 된다.

얼마나 빠를까

데이터를 순회할 때 마다 순회할 데이터의 개수가 1개씩 줄어든다.

데이터 요소가 N개라면, n-1회, n-2회, n-3회 ... 1회.

따라서 n-1 부터 1까지의 합을 구하면 버블 정렬의 비교연산 횟수가 된다.

오래걸리지만 구현은 간단하다는 장점이 있다.

선택정렬의 경우, 한 사이클을 돌면서 교환(Swap)을 딱 1번만 한다. 

교환 할 요소의 인덱스를 기억해 두었다가 내부 for문이 종료되면 교환을 1번 하기 때문이다. 

반면 버블정렬은 가장 큰수를 가장 마지막 자리로 보내는데에 1번 이상이 필요하다.

버블 정렬은 시간 복잡도가 매우 큰 정렬 방식이다. 

버블정렬 코드

#include <stdio.h>

void BubbleSort(int dataset[], int num){ // 배열과 배열길이를 입력받음

    int i = 0, j=0, temp = 0;
    
    for(i=0; i<num-1; i++){ // num-1 만큼 순회  
        
        for(j=0; j<num-(i+1); j++){ // 정렬할 요소가 1개씩 줄어든다 
            
            if(dataset[j] > dataset[j+1]){ // 교환 조건
                temp = dataset[j];
                dataset[j] = dadtaset[j+1];
                dataset[j+1] = temp;
            }
        }
    }
}

int main(){
    
    int dataset[] = {10, 5, 1, 15, 4, 8, 9};
    int num = sizeof(dataset) / sizeof(dataset[0]);
    int i = 0;
    
    BubbleSort(dataset, num);
    
    for(i=0; i<num; i++){
        printf("%d ", dataset[i]);
    }
    
    return 0;
}