상호 배타적 집합
모집합이 여러 작은 집합들로 나뉜 상황을 표현하는 독특한 트리
상호 배타적 집합(Disjoint-Set)을 표현하는 유니온 파인드(Union-Find) 자료구조
유니온-파인드는 '합집합 찾기'라는 의미를 가지고 있다.
서로소 집합 알고리즘 이라고도 한다. (1외에 공약수 없음)
n 명의 사람 중에서 생일이 같은 사람들끼리 팀을 구성하는 상황을 생각해보자.
생일이 여러 달에 속한 사람은 없다. 따라서 2개 팀에 속한 사람이 없다.
유니온 파인드 자료구조는 상호 배타적인 부분 집합들로 나눠진 원소들을 저장하고 조작하는 자료구조다.
유니온 파인드 연산 3가지
n명의 사람을 0번부터 n-1번 까지의 원소로 표현한다.
각 1개의 원소를 포함하는 n개의 집합을 만든다. (초기화)
두 사람 a, b가 생일이 같다는 것을 확인 할 때마다 두 사람이 포함된 집합이 합쳐진다.(Union 연산)
어떤 원소 b가 주어졌을 때, 이 원소가 속한 집합을 반환한다. (Find 연산)
트리로 상호 배타적 집합 표현하기
- 한 집합에 속하는 원소를 하나의 트리로 묶어준다.
- 트리의 루트에 있는 원소를 각 집합의 대표라고 부른다.
- 각 트리의 루트를 찾은 뒤, 하나를 다른 한쪽의 자손으로 넣으면 된다.각 원소가 포함된 트리의 루트를 찾은 뒤 이들이 같은지 비교하기
- 루트가 같다면 같은 트리에 속한 것
- 두 원소가 같은 트리에 속해 있는지 어떻게 확인할까?
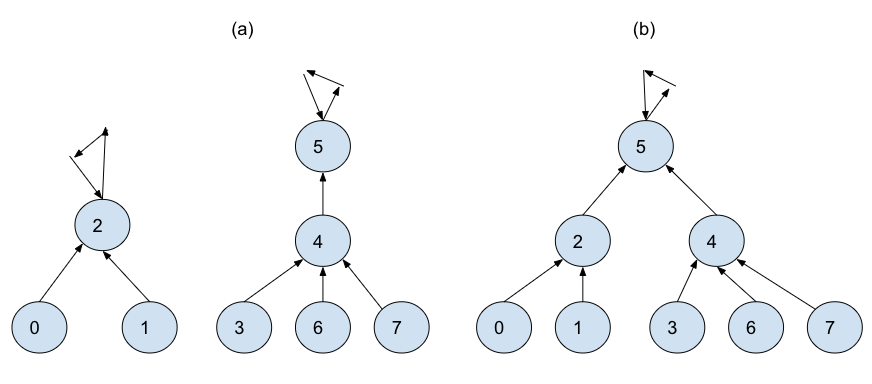
- Find(찾기) 연산루트는 부모가 없으므로 자기 자신을 가리킨다.
- 3의 부모는 4, 4의 부모는 5, 5의 부모는 5 자신이다. 재귀함수로 구현한다.
- 모든 자식 노드가 부모에 대한 포인터를 가져야 한다.
- Union(합치기) 연산한 노드를 다른 노드의 자식으로 넣기 전에 먼저 양 트리의 루트를 찾아야 한다.
- 각 트리의 루트를 찾고, 하나를 다른 한쪽의 자손으로 이어준다.
그림으로 보는 Union-Find (벡터로 구현)
- 초기화노드 i의 부모 노드를 P[i]에 저장한다.
- 처음에 모든 노드의 부모는 자기 자신이다.
-
- Union
)4의 부모는 3으로 변경된다.)Union 연산이 끝난 후, 배열은 다음과 같이 갱신된다.
- 1, 2, 3의 부모는 모두 1이므로, 세 정점은 같은 집합에 속한다.
- 3의 부모는 2가 된다.
- 1, 2, 3이 연결된다면?
- 2의 부모는 1로 변경된다.
- Union(1, 2) , Union(3, 4) 연산으로 노드를 2개씩 합친다.
- Find
- 자신이 속한 집합의 루트를 알아내기 위해 재귀 함수가 사용된다.
(코드) 트리로 상호 배타적 집합 구현
struct NaiveDisjointSet{
vector<int> parent; // 자신의 부모의 번호를 저장
NaiveDisjointSet(int n): parent(n){
for(int i = 0; i < n; i++){ // 처음에는 자기 자신이 자신의 부모다. (혼자니까)
parent[i] = i; // 자신이 어떤 부모에 포함됬는지 기록
}
}
// u 가 속한 트리의 루트의 번호를 찾아서 반환 // 트리의 높이에 비례하는 시간이 걸린다
int find(int u) const{
if(u == parent[u]){ // u가 부모라면
return u;
}
return find(parent[u]);
}
// u가 속한 트리와 v가 속한 트리를 합친다
void merge(int u, int v){
u = find(u); // 양 트리의 루트를 찾아낸다
v = find(v);
if(u == v) return; // u와 v가 같은 트리에 속한 경우 종료.
parent[u] = v;
}
}; union은 예약어이므로 함수명으로 사용할 수 없다.
상호 배타적 집합의 최적화
- 트리를 사용하니까 연산 순서에 따라 한쪽으로 기울어질 수도 있다는 문제가 있다.
- 그러면 Find 연산도 Union 연산도 시간 복잡도 O(n)이 된다.
랭크에 의한 합치기(union-by-rank)
기울어진 트리를 피하기 위해, 항상 높이가 더 낮은 트리를 더 높은 트리 밑에 집어넣자.
(코드) 최적화된 상호 배타적 집합의 구현
rank[] 는 해당 노드가 한 트리의 루트인 경우, 해당 트리의 높이를 저장하는 배열
두 노드를 합칠 때, 높이가 낮은 쪽을 높은 쪽 트리의 서브트리로 포함시킨다.
두 트리의 높이가 같다면, 결과 트리의 높이를 1 증가시킨다.
struct OptimizedDisjointSet{
vector<int> parent; // 자신의 부모의 번호를 저장
vector<int> rank; // 높이를 저장
OptimizedDisjointSet(int n): parent(n), rank(n, 1){
for(int i = 0; i < n; i++){
parent[i] = i;
}
}
// u 가 속한 트리의 루트의 번호를 찾아서 반환
int find(int u) const{
if(u == parent[u]){ // u가 부모라면
return u;
}
return parent[u] = find(parent[u]); // 재귀호출 하면서 parent벡터 업데이트
}
// u가 속한 트리와 v가 속한 트리를 합친다
void merge(int u, int v){
u = find(u); // 양 트리의 루트를 찾아낸다
v = find(v);
if(u == v) return; // u와 v가 같은 트리에 속한 경우 종료.
// v를 u의 자식으로 넣는다.
if(rank[u] > rank[v]) swap(u, v);
// u를 v의 자식으로 넣는다.
parent[u] = v;
// 높이가 같으면 결과 트리의 높이를 1 증가
if(rank[u] == rank[v]) ++rank[v];
};
[출처]
알고리즘 문제해결전략 (구종만 저) 트리 챕터 상호배타적집합 코드
728x90
'알고리즘 > 알고리즘 C' 카테고리의 다른 글
| 이진 탐색 트리 Binary Search Tree (linked list) (0) | 2020.03.18 |
|---|---|
| 이진 탐색 (0) | 2020.03.18 |
| 수식 이진 트리 (Expression Binary Tree) (0) | 2020.03.11 |
| 이진 트리 (0) | 2020.03.11 |
| 트리 기초 (0) | 2020.03.11 |





