'우선순위 큐' 태그의 글 목록

우선순위 큐

우선순위 큐 2020.06.03

우선순위 큐

2020. 6. 3. 10:23

우선순위 큐

보통의 큐 인데 '우선순위'속성을 갖는 자료구조이다.

삽입(Enqueue) 할 때 데이터에 우선순위를 부여한다.

삭제(Dequeue) 할 때 가장 높은 우선순위를 갖는 요소부터 제거한다.

우선순위 큐의 삽입 연산

최소값이나 최대값을 우선순위 기준으로 둔다.

새 요소가 들어오면 값에 따라 적당한 위치를 탐색해야 한다.

일반적으로 힙 순서 속성을 활용하여 구현한다.

우선순위 큐의 제거 연산

전단을 제거하면 끝난다.
전단에는 우선순위가 가장 높은 값(여기서는 최소값) 이 있기 때문이다.

다음은 우선순위 큐의 구현에 필요한 '힙'에 관한 내용이다.

힙

힙은 힙 순서 속성을 만족하는 완전이진트리다.

힙은 루트노드를 제거하는 최소값 제거 연산과 새 노드 삽입 연산이 있다.

힙 순서 속성이란?

트리 내의 모든 노드가 부모 노드 보다 큰 값을 가진다는 규칙이다.

완전이진트리란?

최고 깊이를 제외한 모든 깊이의 노드들이 완전히 채워져 있는 이진트리다.

힙에서 가장 작은 데이터를 갖는 노드는 루트 노드이다.

힙에 새 노드 삽입하기

힙 순서 속성을 만족시킬 때 까지 부모와 값을 비교한다.

삽입의 과정은 아래와 같다.

힙의 최고 깊이, 최 우측에 새 노드를 삽입한다.
새 노드의 부모와 새 노드를 비교한다. 부모 노드가 값이 더 크다면 종료한다. 그렇지 않으면 다음을 진행한다.
새 노드가 더 작다면, 부모와 위치를 교환한다. 2번으로 간다.

힙의 최소값 삭제

힙의 최소값은 항상 루트노드다.
루트 노드를 삭제하고 나서, 힙 순서 속성을 유지하는 작업이 주를 이룬다.

최소값 삭제 과정은 아래와 같다.

힙의 루트에 최고 깊이 최 우측 노드를 옮겨온다.
옮겨온 노드의 양쪽 자식을 비교하여, 둘 중에 더 작은 자식과 교환한다.
옮겨온 노드가 양쪽 자식보다 작거나, 잎노드가 되면 연산을 종료한다. 그렇지 않으면 2번, 3번을 반복한다.

힙 예제 구현 해보기

링크드리스트 VS 배열

링크드 리스트로 구현하면, "힙의 가장 마지막 노드"를 찾는데 효율적인 답을 찾기 어렵다.
힙은 완전이진트리 이므로 배열인덱스를 통해 자식과 부모의 위치를 찾아내는 데 좋다.

k번 인덱스 노드의 양쪽 자식 노드 인덱스 찾기
- 왼쪽 : 2k + 1
- 오른쪽 : 2k +2
k번 노드의 부모 인덱스 찾기
- (k-1)/2 의 몫

힙의 자료구조

typedef struct Node { // 노드 
    int data;
}HeapNode;

typedef struct Heap { // 힙 
    HeapNode* nodes;
    int capacity; // 힙의 용량
    int usedSize; // 힙에 들어있는 노드 개수  
}Heap;

새 노드 삽입하기

Insert()는 아래 두 함수를 활용한다.

GetParent()는 노드의 인덱스를 입력받아서 부모노드 인덱스를 반환한다.
SwapNodes()는 노드와 부모노드를 교환한다.

void Insert(Heap* H, int newData) { 

    // 1. 최고 깊이 최 우측 노드와 그 것의 부모 노드 인덱스
    int currentPosition = H->usedSize;
    int parentPosition = GetParent(currentPosition);

    // 2. 만약, 힙이 꽉차있다면, 용량 증가 
    if (H->capacity == H->usedSize) {

        H->capacity *= 2;
        H->nodes = (HeapNode*)realloc(H->nodes, sizeof(HeapNode) * H->capacity);
    }

    // 3. 최고 깊이 최 우측 노드에 새 노드 삽입 
    H->nodes[currentPosition].data = newData; 

    // 4. 힙 순서 속성 유지할 때까지 비교 반복
    // 탈출 조건 : 자신이 루트 노드가 된다(인덱스 0). 또는 자신의 값이 부모보다 크거나 같다. 
    while (currentPosition != 0 && H->nodes[currentPosition].data < H->nodes[parentPosition].data) {

        SwapNodes(H, currentPosition, parentPosition); // 자리 교환 

        currentPosition = parentPosition; // 1번 처럼 인덱스 갱신 
        parentPosition = GetParent(currentPosition);
    }

    // 5. 용량 증가
    H->usedSize++; 

    return;
}

힙의 최소값 삭제하기

최소값은 항상 루트노드가 가지고 있다.

함수는 일단 루트노드의 최소값을 기억해 두는 것으로 시작한다.
루트노드 자리에 최고 깊이 최 우측 노드를 복사해서 옮겨둔다.
새로 온 노드는 힙 순서 속성을 만족할 때 까지 자신의 자식 노드와 비교하여 교환을 반복한다.

void DeleteMin(Heap* H, HeapNode* root) { 

    int parentPosition = 0; // 루트노드 자신이 부모로 시작. 루트니까 인덱스 0.
    int leftPosition = 0;
    int rightPosition = 0;

    // root에 최소값을 저장해둔다. 
    memcpy(root, &H->nodes[0], sizeof(HeapNode));
    memset(&H->nodes[0], 0, sizeof(HeapNode));

    H->usedSize--; // 최우측 노드 인덱스 
    SwapNodes(H, 0, H->usedSize); // 루트 자리에 최고 깊이 최우측 노드를 옮겨온다. 

    leftPosition = GetLeftChild(0); // 루트 노드의 왼쪽 자식, 오른쪽 자식 인덱스 
    rightPosition = leftPosition + 1;


    while (1) { // 힙 순서 속성을 만족할 때 까지 루트는 자기 자식과 비교한다.

        int selectedChild = 0; // 1. 부모노드(루트노드)와 교환할 노드의 인덱스를 찾아본다 

        if (leftPosition >= H->usedSize) { 
            // 실제 노드 개수보다 왼쪽자식 인덱스가 같거나 크다 
            // 유의점 : 노드 인덱스는 0부터 시작. 사용량은 1부터 시작
            // 즉, 루트노드는 잎노드가 된 상황. 
            break; 
        }

        if (rightPosition >= H->usedSize) { 
            // 사용 인덱스보다 오른쪽 자식인덱스가 크다
            // 즉, 루트노드에게 오른쪽 자식은 존재하지 않고 왼쪽자식만 있는것임.
            selectedChild = leftPosition; // 타겟은 왼쪽자식 
        }
        else { // 양쪽 자식 존재 

            if (H->nodes[leftPosition].data < H->nodes[rightPosition].data) { 
                // 왼쪽 자식이 작다. 타겟은 왼쪽자식 
                selectedChild = leftPosition; 
            }
            else { // 오른쪽 자식이 작다. 타겟은 오른쪽 자식  
                selectedChild = rightPosition;
            }
        }

        // 2. 값을 보고 교환할 필요가 있는지 확인한다 
        if (H->nodes[selectedChild].data < H->nodes[parentPosition].data) {
            SwapNodes(H, selectedChild, parentPosition);
            parentPosition = selectedChild; // 타겟이 새 부모가 된다. 
        }
        else {
            break;
        }

        // 3. 왼쪽 자식, 오른쪽 자식 인덱스를 갱신한다. 
        leftPosition = GetLeftChild(parentPosition);
        rightPosition = leftPosition + 1;
    }

    // 4. 용량의 반 이하만 쓰고 있다면, 힙 용량을 반으로 줄인다. 
    if (H->usedSize < (H->capacity/2)) {

        H->capacity /= 2; // 줄일 용량 
        H->nodes = (HeapNode*)realloc(H->nodes, sizeof(HeapNode) * H->capacity);

    }

}

힙 예제 전체 코드

헤더파일 heap.h
Insert() 와 Delete()를 포함한 함수가 구현된 heap.cpp
테스트 해보는 heap_test.cpp

heap.h

#ifndef HEAP_H
#define HEAP_H

// 힙 

#include <stdio.h>
#include <memory.h> // memcpy
#include <stdlib.h> // realloc

typedef int ElementType;

typedef struct Node { // 노드 
    ElementType data;
}HeapNode;

typedef struct Heap { // 힙 
    HeapNode* nodes;
    int capacity;
    int usedSize;
}Heap;

Heap* Create(int initialSize);
void Destroy(Heap* H); // 
void Insert(Heap* H, ElementType newData);  // 삽입
void DeleteMin(Heap* H, HeapNode* root); // 최소값 삭제 
int GetParent(int index); // 부모 인덱스 리턴
int GetLeftChild(int index); // 왼쪽 자식 인덱스 리턴
void SwapNodes(Heap* H, int index1, int index2);
void PrintNodes(Heap* H);

#endif

heap.cpp

#include "heap.h"

// 힙 메모리 할당 
Heap* Create(int initialSize) {

    Heap* newHeap = (Heap*)malloc(sizeof(Heap));

    newHeap->nodes = (HeapNode*)malloc(sizeof(HeapNode) * initialSize);
    newHeap->capacity = initialSize;
    newHeap->usedSize = 0;

    printf("size:%d\n", sizeof(HeapNode));

    return newHeap;
}

// 힙 메모리 해제 
void Destroy(Heap* H) {

    free(H->nodes);
    free(H);

    return;
}

// 삽입 
void Insert(Heap* H, int newData) { 

    // 1. 최고 깊이 최 우측 노드와 그 것의 부모 노드 인덱스
    int currentPosition = H->usedSize;
    int parentPosition = GetParent(currentPosition);

    // 2. 만약, 힙이 꽉차있다면, 용량 증가 
    if (H->capacity == H->usedSize) {

        H->capacity *= 2;
        H->nodes = (HeapNode*)realloc(H->nodes, sizeof(HeapNode) * H->capacity);
    }

    // 3. 최고 깊이 최 우측 노드에 새 노드 삽입 
    H->nodes[currentPosition].data = newData; 

    // 4. 힙 순서 속성 유지할 때까지 비교 반복
    // 탈출 조건 : 자신이 루트 노드가 된다(인덱스 0). 또는 자신의 값이 부모보다 크거나 같다. 
    while (currentPosition != 0 && H->nodes[currentPosition].data < H->nodes[parentPosition].data) {

        SwapNodes(H, currentPosition, parentPosition); // 자리 교환 

        currentPosition = parentPosition; // 1번 처럼 인덱스 갱신 
        parentPosition = GetParent(currentPosition);
    }

    // 5. 용량 증가
    H->usedSize++; 

    return;
}


// 최소값 삭제 
void DeleteMin(Heap* H, HeapNode* root) { 

    int parentPosition = 0; // 루트노드 자신이 부모로 시작. 루트니까 인덱스 0.
    int leftPosition = 0;
    int rightPosition = 0;

    // root에 최소값을 저장해둔다. 
    memcpy(root, &H->nodes[0], sizeof(HeapNode));
    memset(&H->nodes[0], 0, sizeof(HeapNode));

    H->usedSize--; // 최우측 노드 인덱스 
    SwapNodes(H, 0, H->usedSize); // 루트 자리에 최고 깊이 최우측 노드를 옮겨온다. 

    leftPosition = GetLeftChild(0); // 루트 노드의 왼쪽 자식, 오른쪽 자식 인덱스 
    rightPosition = leftPosition + 1;


    while (1) { // 힙 순서 속성을 만족할 때 까지 루트는 자기 자식과 비교한다.

        int selectedChild = 0; // 1. 부모노드(루트노드)와 교환할 노드의 인덱스를 찾아본다 

        if (leftPosition >= H->usedSize) { 
            // 실제 노드 개수보다 왼쪽자식 인덱스가 같거나 크다 
            // 유의점 : 노드 인덱스는 0부터 시작. 사용량은 1부터 시작
            // 즉, 루트노드는 잎노드가 된 상황. 
            break; 
        }

        if (rightPosition >= H->usedSize) { 
            // 사용 인덱스보다 오른쪽 자식인덱스가 크다
            // 즉, 루트노드에게 오른쪽 자식은 존재하지 않고 왼쪽자식만 있는것임.
            selectedChild = leftPosition; // 타겟은 왼쪽자식 
        }
        else { // 양쪽 자식 존재 

            if (H->nodes[leftPosition].data < H->nodes[rightPosition].data) { 
                // 왼쪽 자식이 작다. 타겟은 왼쪽자식 
                selectedChild = leftPosition; 
            }
            else { // 오른쪽 자식이 작다. 타겟은 오른쪽 자식  
                selectedChild = rightPosition;
            }
        }

        // 2. 값을 보고 교환할 필요가 있는지 확인한다 
        if (H->nodes[selectedChild].data < H->nodes[parentPosition].data) {
            SwapNodes(H, selectedChild, parentPosition);
            parentPosition = selectedChild; // 타겟이 새 부모가 된다. 
        }
        else {
            break;
        }

        // 3. 왼쪽 자식, 오른쪽 자식 인덱스를 갱신한다. 
        leftPosition = GetLeftChild(parentPosition);
        rightPosition = leftPosition + 1;
    }

    // 4. 용량의 반 이하만 쓰고 있다면, 힙 용량을 반으로 줄인다. 
    if (H->usedSize < (H->capacity/2)) {

        H->capacity /= 2; // 줄일 용량 
        H->nodes = (HeapNode*)realloc(H->nodes, sizeof(HeapNode) * H->capacity);

    }

}

// 현재 노드와 부모 노드 교환 
void SwapNodes(Heap* H, int current, int parent) {

    int copySize = sizeof(HeapNode);
    HeapNode* tempNode = (HeapNode*)malloc(sizeof(HeapNode));

    memcpy(tempNode, &H->nodes[current], copySize);
    memcpy(&H->nodes[current], &H->nodes[parent], copySize);
    memcpy(&H->nodes[parent], tempNode, copySize);

    free(tempNode);

    return;
}

int GetParent(int index) { // 부모의 인덱스를 반환 
    return (int)((index - 1) / 2);
}

int GetLeftChild(int index) { // 왼쪽 자식 인덱스 반환 
    return (index * 2) + 1;
}

void PrintNodes(Heap* H) { // 노드 전체 출력 
    int i = 0;

    for (i = 0; i < H->usedSize; i++) {
        printf("%d ", H->nodes[i].data);
    }
    printf("\n");
}

heap_test.cpp

#include "heap.h"

// 힙 

int main(void) {

	Heap* H = Create(3);
	HeapNode minNode;

	Insert(H, 12); // 6개 삽입 
	Insert(H, 87);
	Insert(H, 111);
	Insert(H, 34);
	Insert(H, 16);
	Insert(H, 75);

	PrintNodes(H);

	DeleteMin(H, &minNode); // 삭제 후 출력 하는 것을 반복 
	PrintNodes(H);

	DeleteMin(H, &minNode);
	PrintNodes(H);

	DeleteMin(H, &minNode);
	PrintNodes(H);

	DeleteMin(H, &minNode);
	PrintNodes(H);

	DeleteMin(H, &minNode);
	PrintNodes(H);

	DeleteMin(H, &minNode);
	PrintNodes(H);

	Destroy(H);

	return 0;
}

실행 화면

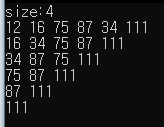
힙을 이용한 우선순위 큐 예제

힙은 최소값이나 최대값을 바로 얻어낼 수 있으므로 우선순위 큐 구현에 적합하다.

힙 예제에 썼던 코드와 우선순위 큐 예제가 다른 점은 아래와 같다.

HeapNode 구조체에 Priority 필드 추가
HeapNode의 data 필드 자료형을 void*로 변경

헤더파일 priorityQueue.h

함수들을 구현한 priorityQueue.cpp

테스트하는 main 함수 priorityQueue_test.cpp 3개로 구성됬다.

실행결과 화면

priorityQueue.h

#ifndef PRIORITYQUEUE_H
#define PRIORITYQUEUE_H

#include <stdio.h>
#include <memory.h>
#include <stdlib.h>

typedef int PriorityType;

typedef struct PQNode {
	PriorityType priority;
	void* data;
}PQNode;

typedef struct PQ {
	
	PQNode* nodes;
	int capacity;
	int usedSize;

}PriorityQueue;

PriorityQueue* PQ_Create(int initialSize);
void PQ_Destory(PriorityQueue* PQ);
void PQ_Enqueue(PriorityQueue* PQ, PQNode newNode);
void PQ_Dequeue(PriorityQueue* PQ, PQNode* root);
int PQ_GetParent(int index);
int PQ_GetLeftChild(int index);
void PQ_SwapNodes(PriorityQueue* PQ, int index1, int index2);
int PQ_IsEmpty(PriorityQueue* PQ);

#endif

priorityQueue.cpp

#include "priorityQueue.h"

// 우선순위 큐 생성 
PriorityQueue* PQ_Create(int initialSize) {
	
	PriorityQueue* PQ = (PriorityQueue*)malloc(sizeof(PriorityQueue));
	PQ->nodes = (PQNode*)malloc(sizeof(PQNode) * initialSize);
	PQ->capacity = initialSize;
	PQ->usedSize = 0;

	return PQ;
}

void PQ_Destory(PriorityQueue* PQ) {

	free(PQ->nodes);
	free(PQ);

	return;
}

// 삽입 
void PQ_Enqueue(PriorityQueue* PQ, PQNode newNode) {

	int currentPosition = PQ->usedSize;
	int parentPosition = PQ_GetParent(currentPosition);

	// 1. 용량 확인 
	if (PQ->usedSize == PQ->capacity) {

		if (PQ->capacity == 0) {
			PQ->capacity = 1;
		}

		PQ->capacity *= 2; // 용량 2배 증가
		PQ->nodes = (PQNode*)realloc(PQ->nodes, sizeof(PQNode) * PQ->capacity);
	}

	// 2. 삽입
	PQ->nodes[currentPosition] = newNode;

	// 3. '힙 순서 속성' 만족시킬 때 까지 후속처리
	while (currentPosition != 0 &&
		PQ->nodes[currentPosition].priority < PQ->nodes[parentPosition].priority) {

		PQ_SwapNodes(PQ, currentPosition, parentPosition); // 자신과 부모 위치 교환 

		currentPosition = parentPosition; // 인덱스 갱신 
		parentPosition = PQ_GetParent(currentPosition);
	}

	PQ->usedSize++;

	return;
}


// 최소값 삭제 
void PQ_Dequeue(PriorityQueue* PQ, PQNode* root) {

	int parentPosition = 0; // 루트노드 자리에서 시작한다. 
	int leftPosition = 0;
	int rightPosition = 0;

	// 1. 루트노드의 값을 root에 저장해둔다. 
	memcpy(root, &PQ->nodes[0], sizeof(PQNode));
	memset(&PQ->nodes[0], 0, sizeof(PQNode)); // 0으로 초기화 

	// 2. 최고 깊이 최우측 노드를 root 자리에 옮긴다. 
	PQ->usedSize--;
	PQ_SwapNodes(PQ, 0, PQ->usedSize);

	leftPosition = PQ_GetLeftChild(0); // 루트의 왼쪽 자식
	rightPosition = leftPosition + 1;  // 루튼의 오른쪽 자식

	// 3. 자신과 자신의 양쪽 자식을 비교 
	while (1) {
		
		int targetPosition = 0;

		// 비교할 자식을 고름 
		if (leftPosition >= PQ->usedSize) { // 자식 없음
			break;
		}
		else if (rightPosition >= PQ->usedSize) { // 왼쪽 자식만 존재 
			targetPosition = leftPosition;
		}
		else {
			// 양쪽 자식 존재 

			if (PQ->nodes[leftPosition].priority < PQ->nodes[rightPosition].priority) {
				targetPosition = leftPosition;
			}
			else {
				targetPosition = rightPosition;
			}

		}

		// 자신과 자식의 값 비교해서 교환 필요 여부 확인 
		if (PQ->nodes[targetPosition].priority < PQ->nodes[parentPosition].priority) {
			PQ_SwapNodes(PQ, targetPosition, parentPosition);
		}
		else {
			break; // 탈출 
		}

		// 인덱스 갱신 
		leftPosition = PQ_GetLeftChild(parentPosition);
		rightPosition = leftPosition + 1;
	}

	// 4. 힙 용량 관리

	if (PQ->usedSize < PQ->capacity / 2) {
		// 용량 감소 

		PQ->capacity /= 2; 
		PQ->nodes = (PQNode*)realloc(PQ->nodes, sizeof(PQNode) * PQ->capacity);
	}

	return;
}

// 노드 교환 
void PQ_SwapNodes(PriorityQueue* PQ, int index1, int index2) {

	int NodeSize = sizeof(PQNode);
	PQNode* tempNode = (PQNode*)malloc(NodeSize);

	memcpy(tempNode, &PQ->nodes[index1], NodeSize);
	memcpy(&PQ->nodes[index1], &PQ->nodes[index2], NodeSize);
	memcpy(&PQ->nodes[index2], tempNode, NodeSize);

	free(tempNode);
	return;
}

int PQ_GetParent(int index) { // 부모 노드 인덱스 반환 
	return (int)((index - 1) / 2);
}
int PQ_GetLeftChild(int index) { //왼쪽 자식 인덱스 반환 
	return (index * 2) + 1;
}

int PQ_IsEmpty(PriorityQueue* PQ) { // 비어서 사용량이 0인지 반환 
	return (0 == PQ->usedSize);
}

priorityQueue_test.cpp

#include "priorityQueue.h"

void PrintNode(PQNode* node) {
	printf("작업명: %s (우선순위:%d)\n", (char*)node->data, node->priority);
}

int main(void) {

	// PQ를 크기를 입력하여 생성한다. 
	PriorityQueue* PQ = PQ_Create(3);

	PQNode Popped;

	PQNode Nodes[7] = {
		{34, (void*)"코딩"},
		{12, (void*)"고객미팅"},
		{87, (void*)"화분물주기"},
		{45, (void*)"문서작성"},
		{35, (void*)"디버깅"},
		{66, (void*)"이닦기"},
	};
	
	// 큐에 넣는다. 
	PQ_Enqueue(PQ, Nodes[0]);
	PQ_Enqueue(PQ, Nodes[1]);
	PQ_Enqueue(PQ, Nodes[2]);
	PQ_Enqueue(PQ, Nodes[3]);
	PQ_Enqueue(PQ, Nodes[4]);
	PQ_Enqueue(PQ, Nodes[5]);

	printf("큐에 남아있는 작업 수 %d\n", PQ->usedSize);

	while (!PQ_IsEmpty(PQ)) {
		PQ_Dequeue(PQ, &Popped);
		PrintNode(&Popped);
	}

	return 0;
}

728x90

저작자표시 비영리 변경금지

'알고리즘 > 알고리즘 C' 카테고리의 다른 글

최소 스패닝 트리 (0)	2020.08.12
그래프의 정의와 표현방법 (2)	2020.08.02
삽입 정렬 (중요) (0)	2020.06.02
버블 정렬 (0)	2020.05.30
균형 이진 탐색 트리 (AVL트리) (1)	2020.03.30

PREV 1 NEXT

JArchive 프로그래밍 일기

우선순위 큐

우선순위 큐

우선순위 큐

우선순위 큐의 삽입 연산

우선순위 큐의 제거 연산

힙

힙 순서 속성이란?

완전이진트리란?

힙에 새 노드 삽입하기

힙의 최소값 삭제

힙 예제 구현 해보기

링크드리스트 VS 배열

힙의 자료구조

새 노드 삽입하기

힙의 최소값 삭제하기

힙 예제 전체 코드

heap.h

heap.cpp

heap_test.cpp

힙을 이용한 우선순위 큐 예제

'알고리즘 > 알고리즘 C' 카테고리의 다른 글

+ Recent posts

티스토리툴바