구간트리
구간트리 (segment tree)
저장된 자료들을 적절히 전처리해 구간에 대한 질문에 빠르게 대답하는 트리
예를 들어, A = {1, 2, 1, 2, 3, 1, 2, 3, 4} 라면,
[2, 4] 구간의 최소치는 1 이다. [6, 8] 구간의 최소치는 2이다.
간단한 알고리즘으로 해당 배열을 순회하여 최소치를 찾아내면 O(n) 의 시간 소요된다.
반면, 해당 배열을 전처리해 구간 트리를 생성하면 같은 연산을 빠르게 구현할 수 있다.
구간트리의 기본 아이디어
구간트리의 기본 아이디어는 주어진 배열의 구간들을 표현하는 이진 트리를 만드는 것이다.
이 때, 루트는 항상 배열의 전체 구간[0, n-1]을 표현한다.
루트의 왼쪽 자식과 오른쪽 자식은 각각 해당 구간의 왼쪽 반과 오른쪽 반을 표현한다.
리프 노드는 길이가 1인 구간을 표현한다.
아래 그림은 배열 길이가 15일 때, 구간 트리의 각 노드가 표현하는 구간들을 보여준다.
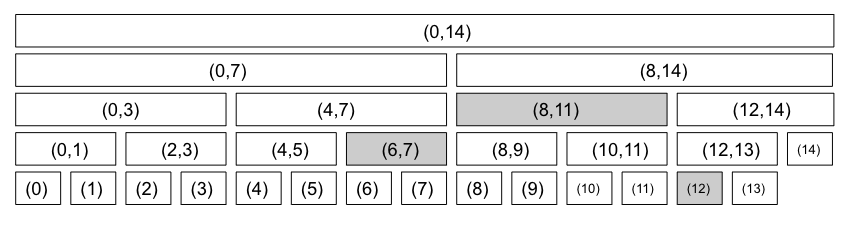
각 노드는 해당 구간에 대한 계산 결과를 저장한다.
예를 들어, 구간의 최소치를 구하는 구간트리는 해당 구간의 최소치를 각 노드에 저장한다.
이러한 전처리 과정을 수행해두면 어떤 구간이 주어지더라도 이 구간을 구간들의 합집합으로 표현할 수 있다.
어떤 구간이 주어지건, 답을 찾기 위해 고려해야 하는 구간의 수는 O(logN)
구간트리의 표현
구간 트리를 다뤄보는 일반적인 예제로 '특정 구간의 최소치를 찾는 문제'가 있다.
구간 최소 쿼리(range minimum query, RMQ) 라고 한다.
구간 트리는 보통 완전이진트리로 표현한다.
(그래서 포인터로 연결된 리스트보다는 배열이 메모리 면에서 낫다.)
루트 노드를 배열의 1번 원소로 표현한다.
노드 i의 왼쪽 자식을 i * 2, 오른쪽 자식을 i * 2 + 1 번째 원소로 표현한다.
배열의 길이 정하는 방법
가장 가까운 2의 거듭제곱으로 n을 올림한 뒤, 2를 곱한다.
(n=6이면, 그 이상의 거듭제곱은 8이다. 따라서 배열의 길이는 16으로 하는 식이다)
귀찮다면 4n 으로 해도 된다. (4n은 모든 경우에 구간트리가 필요로 하는 배열크기보다 크다)
구간 트리의 초기화(init), 질의(query), 갱신(update) 연산을 알아보자.
1. 구간트리의 초기화 : init()
배열 array[] 가 주어지면, 각 노드마다 해당 구간의 최소치를 계산하는 함수 init()을 구현한다.
현재 구간을 2개로 나눠 재귀호출한 뒤, 두 구간의 최소치 중 더 작은 값을 선택해 해당 구간의 최소치를 계산한다.
// 배열의 구간 최소 쿼리 (RMQ) 문제를 해결하는 구간 트리의 초기화
struct RMQ{
// 배열 길이
int n;
// 각 구간의 최소치
vector<int> rangeMin;
RMQ(const vector<int>& array){
}
// node를 루트로 하는 서브트리를 초기화 하고, 이 구간의 최소치를 반환.
int init(const vector<int>& array, int left, int right, int node){
if(left == right)
return rangeMin[node] = array[left];
int mid = (left + right) / 2;
int leftMin = init(array, left, mid, node * 2);
int rightMin = init(array, mid +1, right, node * 2 + 1);
return rangeMin[node] = min(leftMin, rightMin);
}
};노드의 수 만큼의 초기화 시간이 소요된다.
배열의 길이 O(n), 노드의 수 O(n), 초기화 시간 복잡도 O(n)
2. 구간트리의 질의 처리 : query()
구간 트리에서의 순회를 이용해 구현한다.
다음과 같이 질의 함수를 정의한다.
int query(left, right, node, nodeLeft, nodeRight)
/* node가 표현하는 범위 [nodeLeft, nodeRight]와
우리가 최소치를 찾기 원하는 구간 [left, right]의 교집합의
최소 원소를 반환한다. */질의 연산은 아래의 3가지 경우를 처리한다.
- 교집합이 공집합인 경우
- 두 구간은 서로 겹치지 않으니까 반환 값도 없다.
- 반환 값이 무시되도록 아주 큰 값을 반환하도록 하자.
- 교집합이 [nodeLeft, nodeRight]인 경우
- [left,right]가 노드가 표현하는 집합을 완전히 포함하는 경우.
- 이 노드에 미리 계산해 둔 최소치를 곧장 반환하면 된다.
- 이 외의 모든 경우
- 양쪽 자식 노드에 대해 query()를 재귀 호출한 뒤, 이 두 값 중 더 작은 값을 택해 반환한다.
int query(left, right, node, nodeLeft, nodeRight);
/* node가 표현하는 범위 [nodeLeft, nodeRight]와
우리가 최소치를 찾기 원하는 구간 [left, right]의
교집합의 최소 원소를 반환한다. */
const int _INT_MAX = numeric_limits<int>::max();
// 배열의 구간 최소 쿼리를 해결하기 위한 구간 트리의 구현
struct RMQ{
int query(int left, int right, int node, int nodeLeft, int nodeRight){
// 두 구간이 겹치지 않으면 아주 큰 값을 반환한다: 무시됨
if (right < nodeLeft || nodeRight < left) return _INT_MAX;
// node가 표현하는 범위가 array[left .. right]에 완전히 포함되는 경우
if (left <= nodeLeft && nodeRight <= right)
return rangeMin[node];
// 양쪽 구간을 나눠서 푼 뒤 결과를 합친다.
int mid = (nodeLeft + nodeRight) / 2;
return min(query(left, right, node * 2, nodeLeft, mid),
query(left, right, node * 2 +1, mid+1, nodeRight));
}
// query()를 외부에서 호출하기 위한 인터페이스
int query(int left, int right){
return query(left, right, 1, 0, n-1);
}
};아래 그림은 노드가 표현하는 구간과, 최소치를 찾기 원하는 구간이 겹치는 4가지 경우들이다.
노드가 표현하는 구간과 우리가 원하는 구간의 교집합은 짙은 색으로 칠해져 있다.
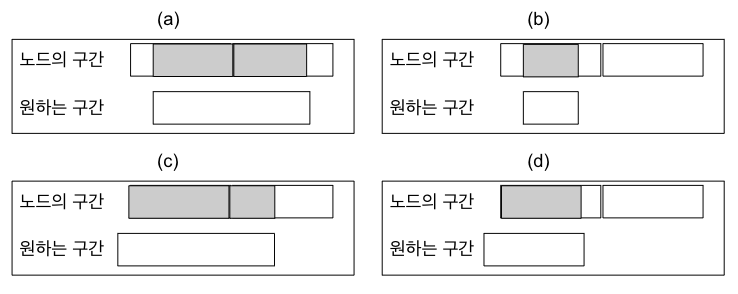
해당 구간이 노드에 완전히 포함되거나(전부 짙은 색) 아예 포함되지 않는다면(전부 옅은 색) 곧장 종료한다.
그림 (b), (c), (d)에서는 재귀 호출했을 때 양쪽 중 하나는 반드시 곧장 종료한다.
따라서, 그림 (a)처럼 두 구간이 겹쳐야만 양쪽 재귀 호출 둘 중 하나도 곧장 종료하지 않고 탐색을 계속하게 된다.
구간은 절반씩 쪼개지므로 질의 연산의 시간복잡도는 O(logN)이다.
3. 구간트리의 갱신 : update()
원래 배열의 index 위치의 값이 newValue로 바뀌었다고 하자.
이 위치를 포함하는 구간은 트리에 O(logN)개 있을것이다.
따라서 O(logN)개만 다시 계산하면 O(logN)시간에 구간트리를 갱신할 수 있다.
- 갱신 과정은 query()와 init()을 합친 것처럼 구현된다.
- 해당 노드가 표현하는 구간에 index가 포함되지 않는다면 그냥 무시한다.
- 포함된다면 재귀 호출해서 두 자식 구간의 최소치를 계산한 뒤, 그 중에서 최소치를 구한다.
struct RMQ{
// .. 생략 ..
// array[index] = newValue로 바뀌었을 때 node를 루트로 하는
// 구간 트리를 갱신하고 노드가 표현하는 구간의 최소치를 반환한다.
int update(int index, int newValue, int node, int nodeLeft, int nodeRight){
// index가 노드가 표현하는 구간과 상관없는 경우엔 무시한다.
if (index < nodeLeft || nodeRight < index)
return rangeMin[node];
// 트리의 리프까지 내려온 경우
if (nodeLeft == nodeRight) return rangeMin[node] = newValue;
int mid = (nodeLeft + nodeRight) / 2;
return rangeMin[node] = min(
update(index, newValue, node*2, nodeLeft, mid),
update(index, newValue, node*2+1,mid+1, nodeRight));
}
// update()를 외부에서 호출하기 위한 인터페이스
int update(int index, int newValue){
return update(index, newValue, 1, 0, n-1);
}
};참고
알고리즘 문제해결전략 (구종만 저)
'알고리즘 > 알고리즘 C' 카테고리의 다른 글
| 펜윅트리 (0) | 2020.08.12 |
|---|---|
| 최소 스패닝 트리 (0) | 2020.08.12 |
| 그래프의 정의와 표현방법 (2) | 2020.08.02 |
| 우선순위 큐 (0) | 2020.06.03 |
| 삽입 정렬 (중요) (0) | 2020.06.02 |